Chapitre I

NOTIONS SUR LES ENSEMBLES

 

1.      Généralités

 

- On distingue sous le nom d’ensemble toute collection d’objets distincts.

- Tout objet d’un ensemble est un élément.

 

2.      Symbole de représentation

 

- Un ensemble se note sous forme de Majuscule: A, E, P…..

- Un élément de l’ensemble se note avec la minuscule de l’ensemble correspondant: a, e, p,…

- Quand un objet a, fait partie d’un ensemble E on dit que a appartient à E:

a  E.

- La non appartenance se note a  E.

- Un ensemble qui n’a pas d’élément est un ensemble vide; on le note .

-Le plus grand ensemble connu est l’ensemble universelle; on le note U.

- Diagramme de VENN-ELLER.

Ce sont des représentations visuelles des ensembles par des ensembles de points dans le plan.

L’ensemble U étant représenté par l’intérieur d’un rectangle, les autres ensembles par des «pataoïdes» à l’intérieur de ce rectangle.

 

 

 

 

 

 

 

                                                                                                                                     

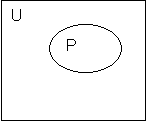
3.      Méthode de définition d’un ensemble

 

Il y a 2 manières pour définir un ensemble

 

a)     Définition par l’énumération:

Un ensemble E est définie lorsque l’on énumère tous les éléments faisant partie de cet ensemble.

Exemple: Soit E = { a, e, i, o, u, y}

On dit aussi: défini en extension.

Le Cardinal: c’est le nombre d’éléments composant l’ensemble. Dans l’exemple précédant C=6.

 

b)     Définition par la Propriété:

Un ensemble E est déterminé lorsqu’on énonce la Propriété qui caractérise les éléments de cet ensemble.

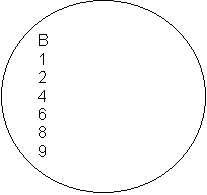
Exemple: B est l’ensemble des éléments x tels que x est entier et > 0.

Définition en compréhension:

L’ensemble E des éléments x tels que x est une lette de l’alphabet et x est une voyelle.

 

Notes:

Dans un ensemble E un même élément ne peut pas figurer plusieurs fois.

Tous les éléments sont rangés de façon arbitraire.

 

4.      Notion de référentiel

 

- Attribut: c’est une propriété qui peut être associée à un objet (un élément).

Exemple: une proposition.

«Les petits pois sont rouges»

C’est une assertion vraie ou fausse

 

- Si on désigne par a un objet et par p une propriété (attribut), on notera p(a) si l’objet vérifie la propriété p.

On peut envisager de rechercher tous les objets pour lesquels une propriété est vérifiée, ces objets constituants un ensemble P appelé alors référentiel.

Exemple: Soit E l’ensemble des prénoms définis en extension.

{Anne, Béatrice, Charles, Denis, Francine, Huy, Irène}

La propriété: les prénoms se terminant par e implique un nouveau référentiel:

E’ {Anne, Béatrice, Francine, Irène}

 

5.      Inclusion et sous-ensemble:

 

- Un ensemble objet: c’est à dire un ensemble peut-être considéré comme un objet et être un élément d’un autre ensemble.

- Soient 2 ensembles A et B, si tous les éléments de A appartiennent aussi à B on dit que A est inclus dans B; on le note A  B.

Exemple: soit l’ensemble B = {1, 2, 3, 4, 5, 6, 7, 8, 9,} et A = {3, 5, 7}

On peut dire A  B.

Remarques:

Si A  B alors B contient A, on note alors B  A.

Si un élément au moins de A n’est pas contenu dans B, il n’y a pas inclusion.

 

Représentations.

	U

 

Inclusion

 

 

 

 

 

 

 

 

 

 

 

 

 

U

Disjonction

 

 

 

 

 

 

 

 

 

 

 

 

 

6.      Opération sur les ensembles

 

- Intersection

On appelle intersection de l’ensemble A et B, l’ensemble J des éléments qui appartiennent à la fois à A et à B.

On note: J = A  B ou (A . B)

 

- Union

On appelle union de l’ensemble A et de l’ensemble B, l’ensemble R des  éléments qui appartiennent à A ou à B.

On note: R = A  B

 

Remarque:

L’inclusion est étroitement lié avec l’intersection et l’union.

A  B implique A  B = A et A  B = B.

 

- Complémentarité

On appelle complémentarité de A par rapport à E l’ensemble des éléments de E n’appartenant pas à A.

On note: CE (A).

S’il n’y a aucune ambiguïté sur E on peut noter CE (A) = A

Remarque:

On sait que si x appartient à A ils satisfait à la relation a.

Inversement si x appartient à CE (A), il ne satisfait pas à la relation a.

 

Lois de l’algèbre des ensembles.

a) Idempotence

A  A = A

A  A = A

 

b) Associativité

(A  B)  C = A  (B  C)

(A  B)  C = A  (B  C)

 

c) Commutativité

A  B = B  A

A  B = B  A

 

d) Distributivité

A  (B  C) = (A  B)  (A  C)

A  (B  C) = (A  B)  (A  C)

 

e) Identité

A  Ø = A

A  U = A

A  U = U

A  Ø = Ø

 

f) Complémentarité

A  A = U

A  A = Ø

U = Ø

 

Autres symboles

Soit une relation p dans un ensemble E, quand tous les éléments de E satisfont à la relation p, on dit « quelque soit x   à  E, x satisfait à P»; on utilise le symbole  et on écrit:

( x) (x  E): p(x)

On l’appelle un quantificateur universel.

Si au moins un élément de E satisfait à la relation P on dit que «Il existe un élément x appartenant à E vérifiant la propriété p»; on utilise le symbole  et on écrit:

( x ) (x  E): p (x)

On l’appelle un quantificateur existentiel.

 

7.      Correspondances et applications

 

Soit deux ensembles A et B. On a une relation de A à B qui affecte à chaque paire d’éléments (a,b) un des énoncés suivants:

a est relié à b.

a n’est pas relié à b.

 

- Correspondance

On dit qu’il y a correspondance si quelque soit a de A, il existe au plus un élément b appartenant à B.

 

- Application

On dit qu’il y a application de A sur B si quelque soit a de A il existe un seul élément b de B.

 

- Injection

Il y a injection si quelque soit b de B il existe un élément a de A au plus.

 

- Surjection

Il y a surjection si quelque soit b de B il existe un élément a de A au moins.

 

Il y a bijection lorsqu’il y a à la fois injection et surjection.